Finding Knight Moves
In a manner similar to finding bishop moves, this piecewise function can be used to find all knight moves.
\[f(x) = \begin{cases} x+1 \text{ if } x = -2 \\ x-1, \text{ if } x = -1 \\ x+1, \text{ if } x = 1 \\ x-1 \text{ if } x=2 \end{cases}\]The domain is: \(\{x \in \mathbb{I} \mid -2 \leq x \leq 2 \text{ and } x \neq 0 \}\)
Half of the possible moves can be found by finding \(f(x)\) for all values in the domain.
To find the remaining directions, use a vertical reflection of the function, \(-f(x)\)
After gathering the possible values, truncate any moves that yield coordinates that do not exist on the board.
Example:
Calculate possible moves for a knight d5.
Current Position: d5 = [5,4]. We refer to this later as \((p_x, p_y)\)
Get all move changes in each direction:
For all values \(x\) in the domain of \(f(x)\) :
moves1 \(= [(-2, f(2)), (-1, f(1)), (1, f(1)), (2, f(2))]\)
moves2 \(= [(-2, -f(2)), (-1, -f(1)), (1, -f(1)), (2, -f(2))]\)
return moves1, moves2
This operation returns the values 1.:
moves1 = \([(-2, -1), (-1,-2), (1,2), (2,1)]\)
moves2 = \([(-2,1), (-1,2), (1,-2), (2,-1)]\)
Find new positions:
For each value-pair \((x_i, y_i)\) in moves1, moves2 and current position \((p_x, p_y)\):
new_position = \((p_x + x_i, p_y + y_i)\)
If new_position is valid: 2
return new_position
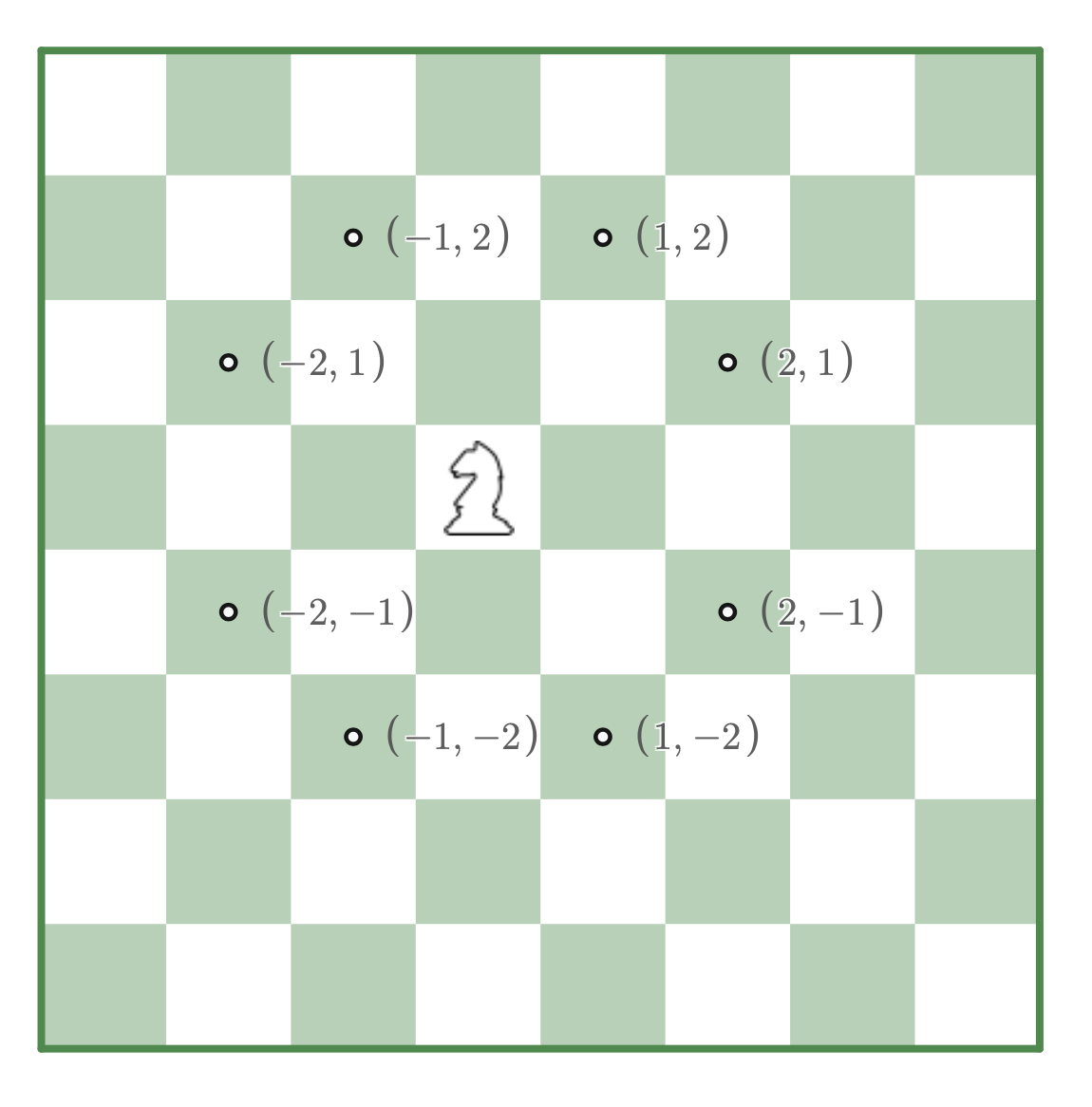
Considering our original position of \([5,4]\), the new positions calculated from moves1 would be: \([1,4], [2,3], [5,7], [6,6]\)
And we map these back to positions 'a4', 'b3', 'e7', 'f6'
(Continue in the manner for moves2)
Graph of knight moves graphed using the piecewise function on desmos
Footnotes: