Finding Bishop Moves
To parse a move for a bishop e.g., Bb3 we have to implicitly disambiguate between our bishops to determine which one can legally move to b3. (Remember that we already know whether it’s black or white’s turn)
There are a couple of approaches available:
First, observe that black’s king bishop and white’s queen bishop can only occupy white squares while black’s queen bishop and white’s king bishop can only occupy black squares.
We could easily devise a table of white and black squares and determine which bishop to move. If it is black’s turn, only the queen bishop can move to b3.
While this approach will work, the intervening squares were not calculated. If white’s king bishop moved from a8 to h1, the path of squares traversed is not known.

Having this information could be useful for calculating the diagonal that the bishop is attacking or defending.
A second, distantly important utility would be an exceedingly rare edge case of same-square bishop disambiguation for an under-promotion event 1.
To achieve this second approach, we perform some some simple arithmetic calculations to find the possible moves a bishop can make. By representing the square positions as x, y coordinate units, we can add or subtract to find intervening squares . In this system, the square(s) a1 is represented as [1,1], h8 = [8,8], a8 = [1,8], and h1 = [8,1]

A new square position can be determined through an arithmetic calculation and then mapping the new position back to a named chess position, e.g., [2,2] = b2.
Calculation example:
Current position: a1 = [1,1]
Movement: [3,3]
New Position [4,4] = d4
This piece-wise function can be used to find all bishop moves, starting with increasing rank and file.
\[f(x) = \begin{cases} x, \text{ if } 1 \leq x \leq 7 \end{cases}\]To find the remaining directions, use horizontal and vertical reflections of the function. Limit the domain of input to \(x\) values between 1 and 7.
-
Increasing rank and decreasing file: \(f(-x)\)
-
Decreasing rank and increasing file: \(-f(x)\)
-
Decreasing rank and decreasing file: \(-f(-x)\)
After gathering the possible values, truncate any moves that yield coordinates that do not exist on the board.
Example:
Calculate possible moves for a black square bishop on a1.
Current Position: d5 = [5,4]. We refer to this later as \((p_x, p_y)\)
Get all move changes in each direction:
For an integer \(x_0\) to \(x_n\) in range \([1..7]\) :
diagonal1 \(= [(x_0, f(x_0), ( x_1, f(x_1), \dots, (x_n, f(x_n)) ]\)
diagonal2 \(= [( -x_0, f(x_0), ( -x_1, f(x_1), \dots, (- x_n, f(x_n)) ]\)
diagonal3 \(= [(x_0, f(-x_0), ( x_1, f(-x_1), \dots, (x_n, f(-x_n)) ]\)
diagonal4 \(= [(- x_0, f(-x_0), ( - x_1, f(-x_1), \dots, (-x_n, f(-x_n)) ]\)
return diagonal1, diagonal2, diagonal3, diagonal4
This operation returns the values 2.:
diagonal1 = \([(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),(7,7)]\)
diagonal2 = \([(-1,1),(-2,2),(-3,3),(-4,4),(-5,5),(-6,6),(-7,7)]\)
diagonal3 = \([(1,-1),(2,-2),(3,-3),(4,-4),(5,-5),(6,-6),(7,-7)]\)
diagonal4 = \([(-1,-1),(-2,-2),(-3,-3),(-4,-4),(-5,-5),(-6,-6),(-7,-7)]\)
Find new positions:
For each value-pair \((x_i, y_i)\) in diagonal1, diagonal2, diagonal3, diagonal4 and current position \((p_x, p_y)\):
new_position = \((p_x + x_i, p_y + y_i)\)
If new_position is valid: 3
return new_position
Considering our original position of \([4,5]\), the new positions calculated from diagonal1 would be: \([5,4], [6,5], [7,6]\)
And we map these back to positions 'e6', 'f7', 'g8'
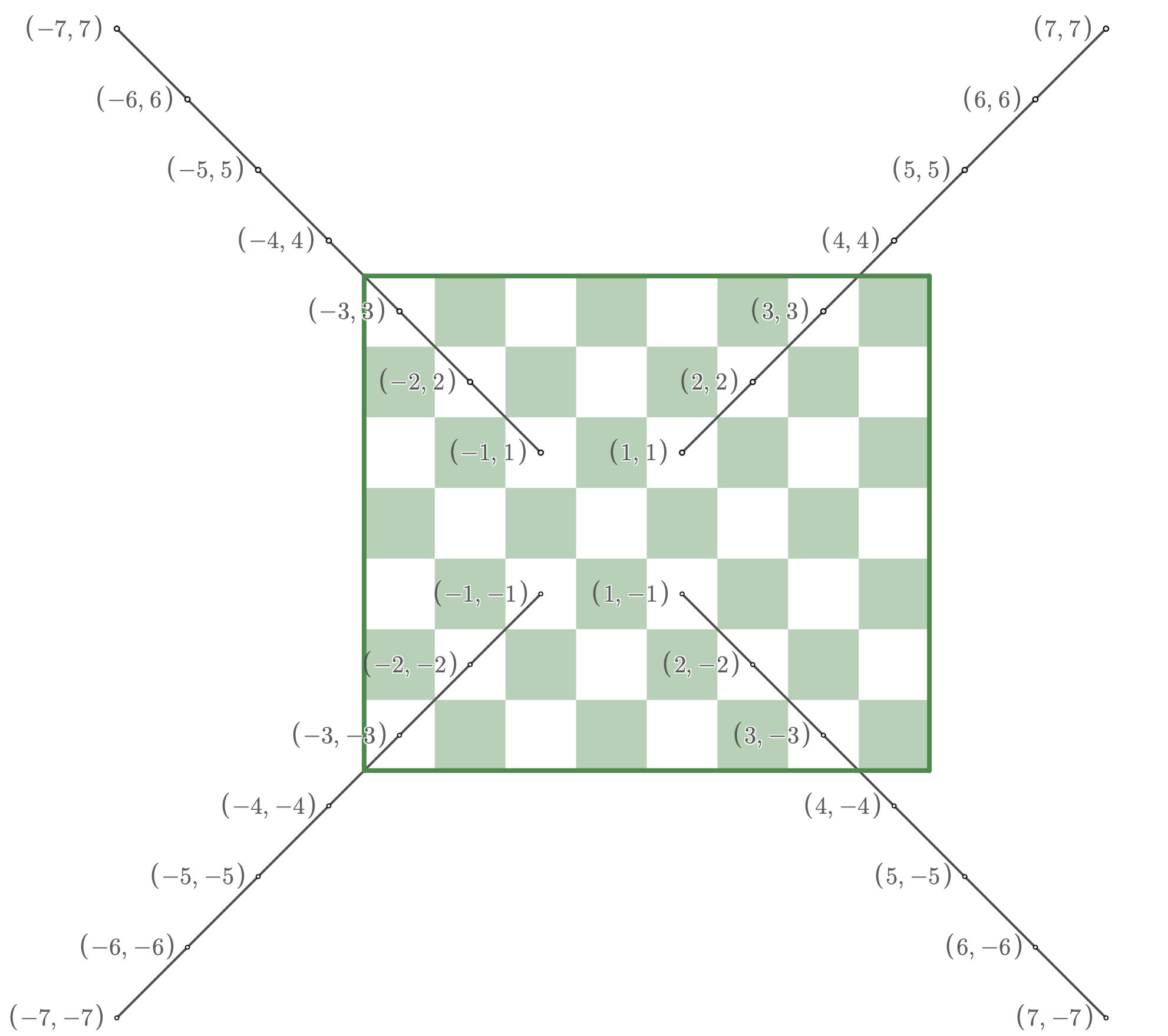
Graph of bishop moves graphed using the piecewise function on desmos
Footnotes:
-
Under promotion to bishop is noteworthy for these championship games where it avoided stalemate. ↩
-
Practically, all of these values could be held in a single list but we keep them separated for cleaner display. ↩
-
A valid position has an \(x\) value between 1-7 and a \(y\) value betwen 1-7 ↩